Page principale

Labyrinthes

Contexte

Je commence à me rendre compte que la difficulté de tout projet ne provient pas uniquement du fait de coder, mais surtout, de l'organisation et de la structure du projet en lui même.
Le sujet que je compte explorer, la génération de labyrinthes me permettra de m'exercer sur ce point précis, à l'aide du moteur de jeu Unity.

De manière plus concrète, l'objectif est de pouvoir générer des labyrinthes avec différentes méthodes et formes, à partir d'une interface utilisateur simple.

Réalisation

Concepts

Définition d'un labyrinthe

^{labyrinthe parfait}

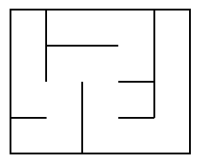
D'après Wikipedia, "Un labyrinthe est un tracé sinueux, muni ou non d'embranchements, d'impasses et de fausses pistes destiné à perdre ou ralentir celui qui cherche à s'y déplacer."
Il y a cependant quelques règles à respecter pour qu'un labyrinthe soit dit "parfait".
Chaque cellule du labyrinthe doit être réliée aux autres et ce, par un chemin unique (on parle de surface connexe). Il ne doit ainsi pas y a avoir de boucles ou de zones fermées.

^{labyrinthe imparfait}

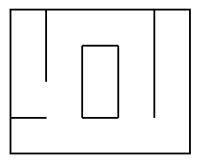
Il existe de nombreuses méthodes pour créer un labyrinthe, une des plus commune est la génération par "suppression de murs".
Le labyrinthe est initialement rempli de murs. Toutes ces zones entourées de murs, sont appelés des cellules.
L'objectif est de relier ces cellules, en supprimant les murs entre elles afin de recréer cette impression de dédale.

Cellule

Dans sa forme la plus simple, une cellule est composée de murs (quatre pour une cellule de forme carrée).
Elle possède également une position, représentée par une coordonée X (axe des abscisses) et une coordonnée Y (axe des ordonnées). Cette position permet de la différencier des autres cellules du labyrinthe.
Nous verrons que certaines méthodes de génération demandent à ce que les cellules possèdent des propriétés supplémentaires.
Par exemple, une valeur indiquant si cette cellule a été visitée ou bien une donnée séparant les cellules en sous-zones du labyrinthe.

Précisions techniques

Le code suivant montre la représentation informatique d'une cellule.
1public class MazeCell
2{
3  public GameObject[] walls;
4  public int x, y;
5
6  public MazeCell(int x, int y)
7  {
8    this.x = x;
9    this.y = y;
10  }
11}
On retrouve les entiers X et Y correspondant aux coordonnées de la cellule.
La taille du tableau walls sera fixée et son contenu assigné pendant la génération d'un tableau rempli de cellules.
L'utilisation de classe rend le concept de cellule extrement modulable. Pour chaque méthode de génération, nous pourrons créer une classe héritant de MazeCell et ainsi n'avoir que les données dont nous avons besoin.

Maintenant que nous avons défini informatiquement ce qu'est une cellule de labyrinthe, nous pouvons commencer à créer une grille constituée de plusieurs de ces cellules.

Tableau de cellules

C'est avec des cellules stockées dans un tableau en deux dimensions que l'on peut représenter notre labyrinthe.

^{labyrinthe vu de dessus}

^{tableau à deux dimensions}

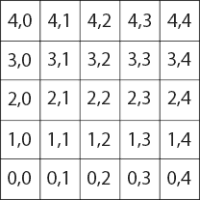
Dans le cas d'un labyrinthe carré, on voit de manière nette la relation avec sa représentation en tableau deux à dimensions.

Habituellement, la position [0, 0] des tableaux à deux dimensions se situe en haut à gauche.
Afin de simplifier le placement de nos cellules dans l'espaces, la position [0, 0] se trouvera en bas à gauche du tableau dans notre cas.
Il sera ainsi plus aisé de convertir les coordonées des cellules dans le tableau (deux dimensions) en coordonnées dans l'espace (trois dimensions).

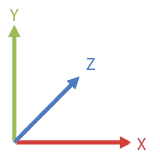^{repère orthonormé de Unity}

^{prefab de cellule}

Maintenant que nous savons comment sont stockées nos cellules dans un tableau, nous pouvons essayer de les placer dans l'espace.
Le plus simple est d'utiliser les "Unity's Prefabs" qui permettent de créer et configurer à l'avance, un objet que nous pourrons réutiliser pendant l'éxecution du programme.
Voici donc le prefab de notre cellule carrée.

D'après notre tableau à deux dimensions, l'espacement entre chaque cellule est de 1 (sur l'axe X et Y), chaque cellule devrait donc faire une taille de 1 par 1.
Cependant, lorsque l'on crée un labyrinthe avec ces dimensions, certaines parois possèdent des angles peu esthétiques.
Passer la taille des murs à 1,1 (les faisant légèrement dépasser de la cellule) nous permet de résoudre ce problème. Les murs des cellules voisines seront désormais superposés.
Cela ne pose pas de problème mais nous verrons comment les supprimer dans le but d'optimiser les performances du programme.

^{angles disgracieux}

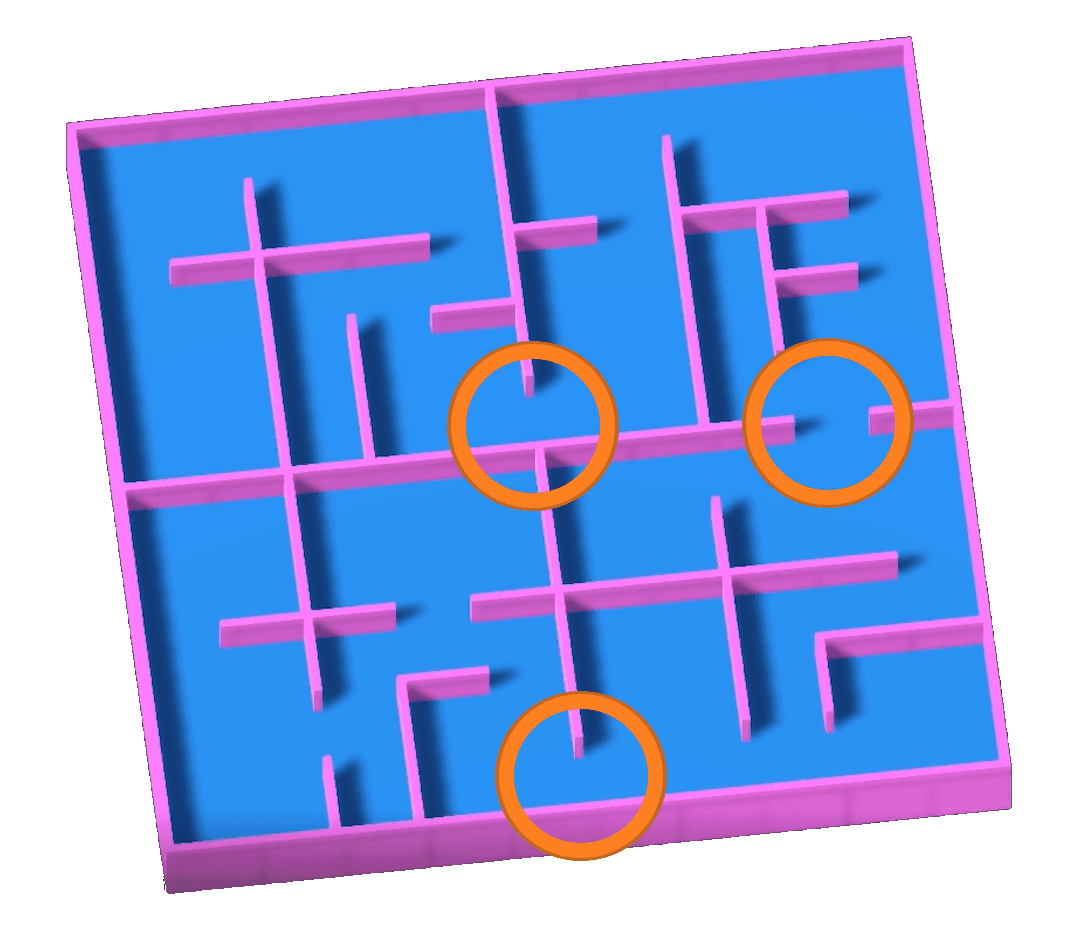
Maintenant que nous possédons notre cellule sous forme de prefab, nous pouvons à l'aide d'une longueur et d'une largeur, faire apparaitre nos cellules.
Il faut pour cela, parcourir chaque case du tableau, de la position [0, 0] à la position [longueur - 1, largeur - 1] (-1, car on compte à partir de 0).

Précisions techniques

Voici le code permettant de créer un labyrinthe rempli de cellules.

1MazeCell[,] maze;
2GameObject cell_prefab;
3int height, width;
4
5maze = new MazeCell[height, width];
6
7for(int y = 0; y < height; y++)
8{
9  for (int x = 0; x < width; x++)
10  {
11    maze[y, x] = new MazeCell(y, x);
12    Vector3 position = new Vector3(y, 0, x);
13    GameObject cell = Instantiate(cell_prefab, position, Quaternion.identity);
14
15    cell.walls = new GameObject[4];
16    maze[y, x].walls[0] = cell.transform.Find("TopWall").gameObject;
17    maze[y, x].walls[1] = cell.transform.Find("LeftWall").gameObject;
18    maze[y, x].walls[2] = cell.transform.Find("BottomWall").gameObject;
19    maze[y, x].walls[3] = cell.transform.Find("RightWall").gameObject;
20  }
21}

A l'aide de la fonction Instantiate de Unity, ce code nous permet de créer une cellule pour chaque case de notre tableau à deux dimensions mais également de l'initialiser pour lui donner ses valeurs.

^{labyrinthe vu de dessus}

^{résultat en 3D}

Suppression de murs entre cellules

^{cellules voisines}

Voyons maintenant comment relier deux cellules voisines.
Relier deux cellules veut en réaliter dire, supprimer les murs qui séparent ces cellules.
Dans l'exemple suivant, nous voulons relier deux cellules voisines horizontalement. Pour ce faire, il faut supprimer le mur de droite de la cellule A et le mur de gauche de la cellule B.

Précisions techniques
Pour nous simplifier la vie, faisons une fonction qui relie deux cellules voisines.
L'objectif est de supprimer le mur de chaque cellule en fonction de la position de son voisin.
1void LinkNeighbors(MazeCell cell_1, MazeCell cell_2)
2{
3  Vector2 dir = new Vector2(cell_1.x - cell_2.x, cell_1.y - cell_2.y);
4
5  if (dir.y == -1)
6    DestroyWalls(cell_1.TopWall, cell_2.BottomWall);
7  else if (dir.y == 1)
8    DestroyWalls(cell_1.BottomWall, cell_2.TopWall);
9  else if (dir.x == -1)
10    DestroyWalls(cell_1.RightWall, cell_2.LeftWall);
11  else
12    DestroyWalls(cell_1.LeftWall, cell_2.RightWall);
13}
14
15void DestroyWalls(GameObject wall_1, GameObject wall_2)
16{
17  Destroy(wall_1);
18  Destroy(wall_2);
19}
C'est à l'aide de la variable dir que nous pouvons savoir comment sont situées nos deux cellules l'une par rapport à l'autre.
Voici un exemple expliquant de manière visuelle, comment la variable dir fonctionne et interprète les coordonnées qu'elle calcule.
A gauche on peut voir les coordonées réelles des cellules, tandis qu'à droite, sont affichées les coordonées relatives à la cellule centrale.
Maintenant que nous savons identifer les cellules voisines, il suffit de supprimer les murs adéquats avec la fonction Destroy de Unity.

Suppresion des murs superposés

Une fois le labyrinthe généré, nous pouvons supprimer les murs superposés restants.
Cela permet d'optimiser l'efficacité du programme en supprimant les murs inutiles.

Précisions techniques
1for (int y = 0; y < height; y++)
2{
3  for (int x = 0; x < width; x++)
4  {
5    if (x < width - 1 && _maze[y, x].RightWall != null && _maze[y, x + 1].LeftWall != null)
6      Destroy(_maze[y, x].RightWall);
7    if (y < height - 1 && _maze[y, x].TopWall != null && _maze[y + 1, x].BottomWall != null)
8      Destroy(_maze[y, x].TopWall);
9  }
10}
Pour chaque cellule, on vérifie qu'elle ne soit pas en bordure du labyrinthe (afin de ne pas ouvrir le labyrinthe).
Si cette cellule possède un mur droit et que la cellule à sa droite possède un mur gauche. On supprime le mur droit de la cellule actuelle.
Le processus est le même pour le mur du bas. Si la cellule scrutée et celle du dessous possèdent leurs murs voisins, on supprime le mur bas de la cellule actuelle.

Voici donc tous les concepts nécessaires pour créer un labyrinthe.
Avant de présenter les algorithmes de génération, voici une section montrant brièvement comment ces concepts peuvent être réutilisés afin de créer des labyrinthes à cellules hexagonales.

Cellules hexagonales

Un hexagone est un polygone à six sommets et six côtés. On retrouve généralement cette forme géométrique sous deux orientations :

^{hexagone "pointy"}

^{hexagone "flat"}

La seule différence avec la celulle carrée est le nombre de murs.
La classe précédemment définie (MazeCell ) reste utilisable, la seule chose à modifier est l'attribution des murs de la cellule.

La dernière question à nous poser est : comment représenter une grille hexagonale dans un tableau à deux dimensions ?
De nombreuses représentations existent déjà avec chacune ses avantages et inconvénients.
La solution choisie ici, est d'utiliser la même méthode que pour les cellules carrées. C'est une représentation simple à mettre en place, cependant, elle s'avère peu pratique lorsque l'on souhaite relier des cellules entre elles.

^{tableau à deux dimensions}

^{grille d'hexagones "flat"}

^{grille d'hexagones "pointy"}

Précisions techniques
Voici la première difficulté des grilles hexagonales. Selon l'orientation de l'hexagone, une cellule sur deux sera décalée.
Sur l'image de gauche on peut constater que sur chaque ligne, un hexagone sur deux se trouve décalé en hauteur.
À droite, ils sont décalés sur l'axe horizontal.
^{Grille d'hexagones "flat"}
^{Grille d'hexagones "pointy"}
Ce choix de représentation nous force donc à différencier les opérations, en fonction de l'orientation de l'hexagone.
Il existe cependant d'autres moyen de stocker ces hexagones dans un tableau.
Ceux-ci sont présentés sur le guide des hexagones de Red Blob Games

Algorithmes

Backtracker

Probablement l'une des plus répandues (car l'une des plus simples), la méthode du backtracker (ou retour arrière en français) permet de systématiquement tester l'ensemble des possibilités.
Cette famille d'algorithmes est utilisée pour résoudre des problèmes algorithmiques comme de l'optimisation combinatoire ou des jeux, telle que le problème des huit dames ou la résolution de sudoku.

Appliquée à nos labyrinthes, en partant d'une grille remplie de murs, cette méthode a pour objectif de créer un chemin, en passant par toutes les cellules du labyrinthe.
De manière plus détaillée :
Chaque cellule du tableau possède un état "visitée" ou non (initialisé à non-visitée). Depuis une cellule de départ, le programme va se déplacer aléatoirement sur une cellule non-visitée, voisine à la sienne (et définir son état comme visitée).
Dès lors qu'une cellule est entourée de cellules visitées, l'algorithme va revenir sur ses pas jusqu'à retrouver des cellules non-visitées.
S'il n'en trouve plus, cela veut dire que toutes les cellules ont été parcourues.

^{illustration de la méthode du backtracker}

Pour garder en mémoire les déplacements effectués, on stocke les cellules visitées dans une pile (une structure de données informatique).

^{représentation d'une pile}

Algorithme :

1 - Choisir une cellule, la marquer comme visitée et l'ajouter à la pile
2 - Tant que la pile n'est pas vide
    1 - Prendre la cellule au sommet de la pile et la considérer comme la cellule actuelle
    2 - Si la cellule actuelle possède au moins un voisin "non-visité"
        1 - Mettre la cellule actuelle au sommet de la pile
        2 - Choisir une des cellules voisines non-visitée
        3 - Relier la cellule actuelle à la cellule choisie
        4 - Définir la cellule choisie comme visitée et la mettre au sommet de la pile

Cette méthode est extrêmement simple à implémenter et plutôt efficace. Elle peut cependant se révéler gourmande en stockage à cause de la taile de la pile, qui augmente en fonction de la surface du labyrinthe à générer.
Un autre inconvénient est le résultat qui se retrouve quelques fois non pas "labyrinthique" mais juste comme un long chemin tortueux, avec peu d'embranchements. Ceci s'explique par le fait que la méthode explore aussi loin que possible chaque possibilité, avant de revenir sur ses pas, limitant ainsi le choix des prochains déplacements.

^{démonstration de la méthode backtracker avec un labyrinthe 10 par 10}

^{démonstration de la méthode backtracker avec un labyrinthe 30 par 30}

Kruskal

L'algorithme de Kruskal est initialement appliqué dans le domaine des graphes.
Il permet de rechercher un arbre recouvrant le poids minimum dans un graphe.
Des applications concrètes que l'on pourrait lui trouver, seraient de simplifier un câblage ou bien de supprimer les chemins de transports les moins rentables.

Cette méthode est une version aléatoirisée de l'algorithme d'origine.
Initialement la méthode sélectionne les arêtes d'un graphe par poids croissant.
Or ici, elles seront séléctionnées de manière aléatoire.

^{illustration de la méthode de Kruskal}

Plus concrètement, à partir d'un labyrinthe rempli de murs, chaque cellule possède un set (un identifiant unique).
L'objectif est de relier les cellules de sets différents et d'appliquer un set commun aux cellules réliées.

Algorithme :

1 - Tant que toutes les cellules n'ont pas le même set
    1 - Prendre deux cellules voisines avec un set différent
    2 - Relier ces deux cellules
    3 - Agrandir le set de l'une des deux cellules sélectionnées en affectant ce set à l'autre cellule et aux cellules de son propre set

Cet méthode est plutôt simple et directe. Elle peut cependant se révéler coûteuse, notamment lorsqu'il faut changer le set d'un groupe de cellules.
La manière la plus simple est d'itérer sur toutes les cellules du labyrinthe. Il est cependant possible d'utiliser des listes chainées ou d'autres structures de données pour isoler les sets afin d'alléger cette opération.

Dans sa finalité, l'algorithme de Kruskal créé de nombreuses impasses peu profondes.

^{démonstration de l'algorithme de Kruskal avec un labyrinthe 10 par 10}

^{démonstration de l'algorithme de Kruskal avec un labyrinthe 30 par 30}

Prim

La méthode de Prim a de nombreuses ressemblances avec celle de Kruskal : son objectif est similaire, mais la manière de l'atteindre est fondamentalement différente.
Cet algorithme permet également de trouver un arbre recouvrant le poids minimum dans un graphe.
Là où la méthode de Kruskal sélectionne les arrêtes de poids faibles dans tout le graphe, Prim va, depuit un point de départ, faire croître un abre en sélectionnant les arêtes de poids faibles incidentes à cet arbre.

Encore une fois, cette méthode est aléatoirisée par rapport à l'algorithme d'origine.
Au lieu de choisir l'arête la plus faible, elle sera choisie de manière aléatoire.

Pour appliquer ce concept à nos labyrinthes, il va falloir garder en mémoire :
Premièrement, les cellules visitées
Puis, les cellules voisines des cellules visitées (que nous appelerons les cellules "en bordure")

A partir d'une cellule de départ, le programme va relier une cellule en bordure à une cellule visitée.
Cela aura pour effet de faire croître une "zone" qui va petit à petit, former notre labyrinthe en supprimant les murs de aléatoirement.

^{illustration de la méthode de Prim}

Algorithme :

1 - Choisir une cellule de départ et noter cette cellule comme visitée
2 - Noter ses cellules voisines comme bordure
3 - Tant qu'il existe des cellules en bordure
    1 - Choisir aléatoirement une des cellules en bordures
    2 - La relier à une cellule visitée voisine
    3 - Noter cette cellule comme visitée et marquer ses voisines (non-visités) comme bordure

Sans grande surprise, le résultat est similaire à celui de Kruskal.
Le labyrinthe possède ici aussi de nombreuses impasses peu profondes.

^{démonstration de la méthode de Prim avec un labyrinthe 10 par 10}

^{démonstration de la méthode de Prim avec un labyrinthe 30 par 30}

Divisions récursives

Pour la première fois, nous partirons d'un labyrinthe sans murs à l'intérieur !
Cette méthode consiste à découper notre labyrinthe en une multitude de salles (que l'on nommera "chambres").

Le concept et son implémentation sont on ne peut plus simples.
Il faut diviser chaque chambre en quatre à l'aide de murs. Pour que les nouvelles chambres ne soient pas inaccessibles, il faut veiller à laisser un passage dans les murs créés.

^{illustration de la méthode des divisons récursives}

Il est possible de rendre le résultat un peu plus intéressant en divisant les chambres, non plus au milieu, mais de manière aléatoire.

Algorithme :

1 - Depuis la chambre initiale, créer deux murs perpendiculaires (de sorte à créer 4 sous-chambres)
    2 - Créer un passage dans trois des quatre murs
    3 - Si il est possible de diviser une sous-chambre
        1 - Retourner à l'étape 1 pour cette sous-chambre

Le style de ce labyrinthe est très différent de ceux vus précédemment
Cette méthode a tendance à créer de longs couloirs, ce qui rend la résolution du labyrinthe plus aisée, notamment car les séparations entre les chambres sont extrêmement appararentes.

Ce concept si simple, peut être légèrement modifié pour obtenir d'autres résultats.
Il est par exemple possible de mettre une limite de recursivité afin d'obtenir des salles plus grandes.

^{démonstration de la méthode récursive avec un labyrinthe 10 par 10}

^{démonstration de la méthode récursive (aléatoirsée) avec un labyrinthe 20 par 20}

^{démonstration de la méthode récursive avec un labyrinthe 80 par 80}

^{démonstration de la méthode récursive (aléatoirisée) avec un labyrinthe 100 par 100}

Divisions récursives améliorées

Pour finir, voici un algorithme de Jamis Buck, reprenant le concept de la méthode récursive.

L'algorithme précédent, rend les passages entre les zones du labyrinthe extrêmement visibles.
En repérant ce passage, il est possible de faire le chemin à l'envers et de trouver la solution.

Il est à noter que tous les labyrinthes possèdent ces passages. S'ils sont facilement repérables ici, c'est à cause des longs murs créés pour séparer les chambres.

^{séparations trop visibles entre les chambres}

L'objectif de cette nouvelle méthode est de rendre moins évidente la séparation des zones du labyrinthes, tout en gardant les propriétés de la méthode récursive.

La solution trouvée par Jamis Buck consiste a aléatoiriser la forme des chambres. Au lieu d'avoir une surface rectangulaire, la chambre pourra être de n'importe quelle forme.
C'est de cette manière qu'il réussit à "casser" le quadrillage de la méthode récursive basique.

^{illustration de la méthode de divisions récursives améliorée}

La manière de trouver la forme de la chambre est assez atypique.
La forme d'une chambre est désormais définie par une région.
Une région, est un ensemble de cellules, voisines les unes des autres. (Il ne peut donc pas y avoir de cellule non-reliée à la région). Initialement, toutes les cellules du labyrinthe forment une région.
Pour séparer cette chambre, il faut créer deux sous-régions.

La manière dont ces sous-régions se partagent les cellules de la région principale est la suivante :
Au début, chaque sous région commence depuis une cellule choisie au hasard.
Les sous-régions s'étendent ensuite aléatoirement sur les cellules voisines.
Ce processus se termine dès lors qu'il ne reste plus de cellule non affectée à une sous-région.
C'est ainsi que nous nous retrouvons avec une chambre donc la séparation n'est plus aussi régulière et évidente que précédemment.

Le reste est assez similaire à la méthode récursive initiale.
Une fois les sous-régions séparées et le passage entre elles créé, le processus se répète de manière récursive pour chaque sous-région.

Algorithme :

1 - Former une région contenant toutes les cellules du labyrinthe
2 - Séparer la région de la manière suivante :
    1 - Choisir deux cellules de départ dans la région initiale et les assigner à une liste
    2 - Choisir au hasard une cellule dans la liste puis la retirer de la liste
    3 - Pour tous les voisins de la cellule choisie, si ils ne sont pas déja dans une sous-région
        1 - Les rajouter à la liste
        2 - Assigner chaque voisin à la sous-région de la cellule choisie
    4 - Répéter les étapes 2.2 et 2.3 jusqu à ce que la région soit séparéee
3 - Construire un mur séparant les deux sous-régions tout en laissant un passage dedans
4 - Répéter 2 et 3 de manière récursive pour chaque sous région

En limitant le nombre de récursions, il est possible de faire varier la taille des chambres. A la place de n'avoir que des couloirs, il est désormais possible d'avoir des "salles" dans le labyrinthe. Ce qui change des générations vues auparavant.

En limitant la profondeur de récursivité, il se peut qu'une chambre apparaisse au milieu d'une zone et qu'elle ne soit donc pas connectée au reste des murs du labyrinthe.
Lorsque les deux sous-régions cherchent à s'étendre, il arrive que l'une d'entre elles entoure l'autre, ce qui crée un îlot.
Pour éliminer ces cas, il faut modifier l'étape 2.1 de l'algorithme.
En plus de choisir aléatoirement une cellule depuis la liste, il faut en plus vérifier que celle-ci se trouve en bordure de la région.
Il est désormais impossible que ces îlots se forment car les cellules de départs sont toujours rattachées au reste du labyrinthe.

^{démonstration de la méthode récursive améliorée avec un labyrinthe 10 par 10}

^{démonstration de la méthode récursive améliorée avec un labyrinthe 30 par 30}

^{démonstration de la méthode récursive améliorée (profondeur limitée) avec un labyrinthe 30 par 30}

Structure du projet

Comme annoncé au début, l'objectif est de structurer le mieux possible ce projet.

L'idée est d'avoir quelque chose d'extrêmement modulable et améliorable, afin de pouvoir rajouter ou bien modifier des éléments sans détériorer le travail existant.

Pour l'utilisateur, le plus pratique est d'avoir une interface, offrant la possibilité de sélectionner et modifier :

La forme des cellules
Les dimensions du labyrinthe
La méthode de génération
D'autres paramètres, liés à la méthode choisie

C'est cette interface qui, après avoir récolté les entrées de l'utilisateur, va transmettre les informations pour générer le labyrinthe demandé.

Dans ce projet, le fait d'avoir plusieurs formes de cellules, oblige à réecrire les méthodes de génération pour chacune.
Le plus simple est donc de créer un intermédiaire pour chacune de ces formes.
Cet intermédiaire aura pour rôle, de transmettre les informations récoltées par l'interface, à la méthode choisie, mais également de générer le labyrinthe rempli de murs (si nécessaire).

^{Schéma structure}

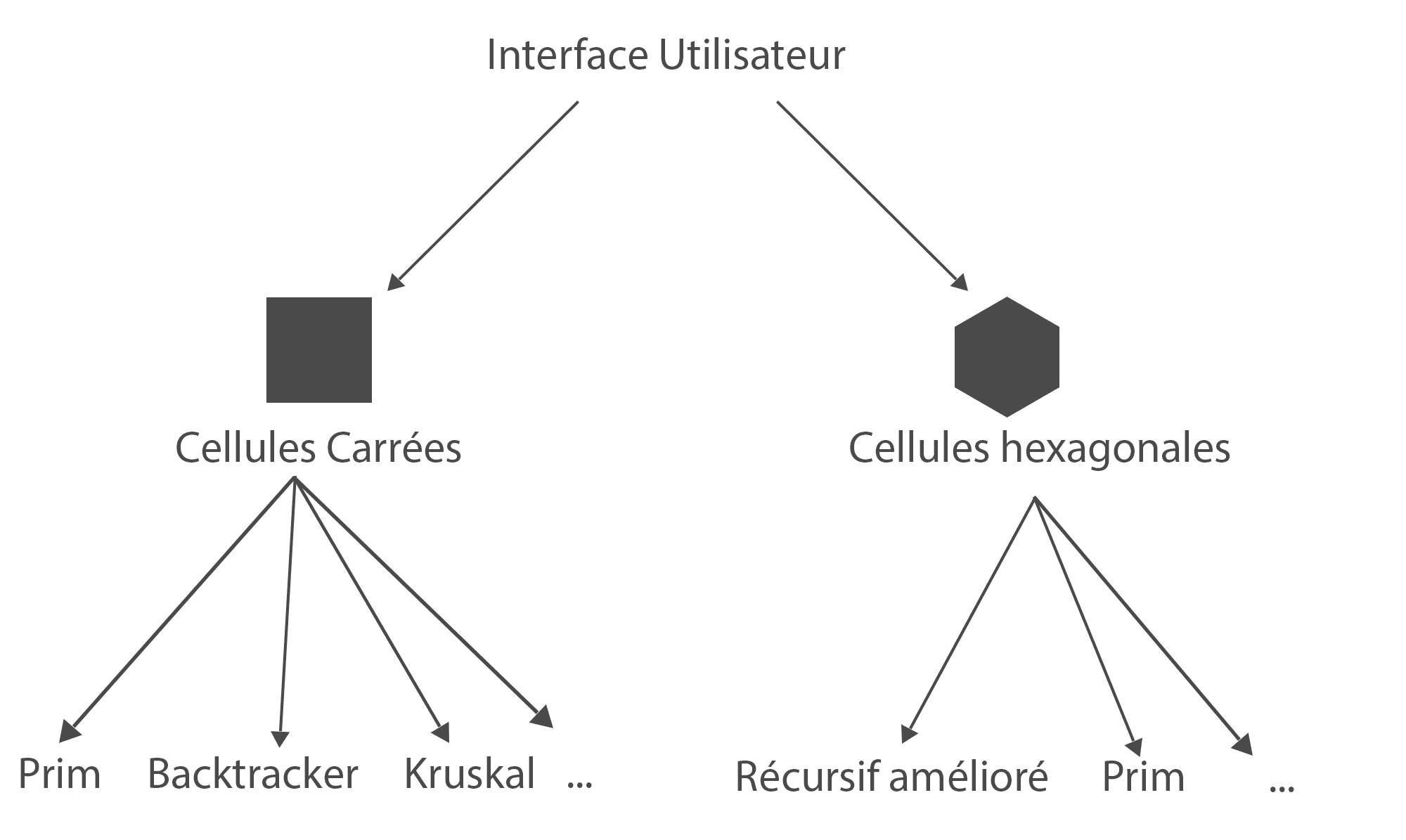
Ce modèle permet de rajouter des méthodes de génération pour chaque forme de cellule.
Il permet également d'implémenter de nouvelles formes sans altérer le fonctionnement de ce qui existe déjà.

Conclusion

En travaillant sur ce projet les week-ends et quelques heures par semaines il m'a fallu 2 mois pour considérer ce projet comme stable et terminé.

Il est cependant possible d'améliorer et d'optimiser certaines méthodes de génération mises en place. Quelques-unes, comme la récursive améliorée ou la méthode de Kruskal sont assez demandeuses en ressources.

Avec du recul, je me rends compte que j'ai seulement gratté la surface de la génération de labyrinthes.
Il existe une infinité de méthodes avec toutes leurs spécificités, avantages et inconvénients.
Pour rendre ce projet un peu plus complet, il est possible de rajouter d'autres méthodes de génération ainsi que d'autres formes de cellules (triangulaires, circulaires, etc ...)

Une suite à ce projet pourrait être de résoudre les différents labyrinthes créés.

Sources

Menu

Page principale

Labyrinthes

Contexte

Réalisation

Concepts

Définition d'un labyrinthe

Cellule

Tableau de cellules

Suppression de murs entre cellules

Suppresion des murs superposés

Cellules hexagonales

Algorithmes

Backtracker

Kruskal

Prim

Divisions récursives

Divisions récursives améliorées

Structure du projet

Conclusion

Sources

Backtracker

Kruskal

Prim

Récursif

Récursif amélioré

Téléchargement

Code source

Téléchargement