Rhythmic diffusion

Analyze audio

Sommaire

• Introduction
• Lecteur audio
• Décomposition d'un signal audio
• Détection de variation d'intensité
• Répartition des différentes fréquences
• Regroupement des variations d'intensité
• Calcul des ratios
• Conclusion

Introduction

Dans cette partie, l'objectif est de pouvoir jouer un fichier audio pendant l'exécution de la réaction-diffusion précédemment créée.
Mais ce n'est pas tout, pour par la suite influencer la simulation en fonction de la musique jouée, il faut choisir quelles informations audio extraire en temps réel.

Cette partie est conçue pour fonctionner avec plusieurs styles de musique, tel que le genre post-rock, électronique mais surtout techno. C'est pourquoi, le choix qui a été fait est d'obtenir un ratio décrivant l'intensité de la basse, un autre pour les cymballes et un dernier plus général pour les sonorités autres.

Ces ratios permettent de décrire simplement l'état des caractéristiques correspondantes et par la suite de les utiliser pour modifier divers paramètres de la simulation en conséquence.

Lecteur audio

Il existe un grand nombre de bibliothèques externes permettant de jouer des sons en C++, celles-ci offrent généralement un grand nombre de fonctionnalité supplémentaires (traitement audio, gestion MIDI, émulation d'instruments, ...).

Le traitement du signal sera (presque) entièrement fait à la main, la seule chose que doit posséder la librairie est un moyen de pouvoir jouer un fichier audio en laissant donnée brute du son accessibles.
La librairie, "Synthesis Toolkit (STK)" répond à ces simples critères. Un code d'exemple permettant de lire un fichier audio est même fournit dans les sources.

Le type de fichier requis par la bibliothèque est le "Waveform Audio File Format" (WAV).
A la différence du format MP3 ou OGG, celui-ci n'utilise pas de compression pour réduire la taille de ses données, mais reste largement utilisé, principalement pour sa structure en blocs de données.

Le fonctionnement de la lecture audio utilise un mécanisme de fonction de rappel (ou "callback").
Le système audio de l'ordinateur va appeler la fonction qui a été spécifiée avant de commencer de la lecture, quand celui-ci à besoin de plus de données pour continuer à jouer le fichier audio sans interruptions.
C'est dans cette fonction de rapel que le curseur de lecture du fichier est avancé, et que les données brutes sont transmises au système audio.

Il est donc assez simple à partir d'ici, de créer un simple lecteur audio permettant de lancer, stopper, metter en pause et même avancer / reculer la lecture d'un fichier audio.

Décomposition d'un signal audio

Maintenant qu'un morceau peut être joué dans l'application, il est temps de s'intéresser aux données passées au système audio.
A chaque fois que la fonction de rappel est exécutée, mille vingt-quatre nombres entre moins un et un sont transmis par cette fonction.
C'est le système audio qui va ensuite interpréter ces valeurs pour produire le son décrit par celles-ci.

En l'état, ces données ne donnent pas d'information sur l'intensité du son, ou les fréquences utilisées.
Il est cependant possible de passer du domaine temporel au domaine fréquentiel en utilisant la fonction mathématiques appelée "Transformation de Fourier".
La transformée de Fourier convertit la fonction décrite par les mille vingt-quatre valeurs en plusieurs ondes sinusoïdales représentant chacune, différentes fréquences présente dans le signal décrit par ces mille vingt-quatre valeurs.

^{Domaine temporel vs domaine fréquentiel}

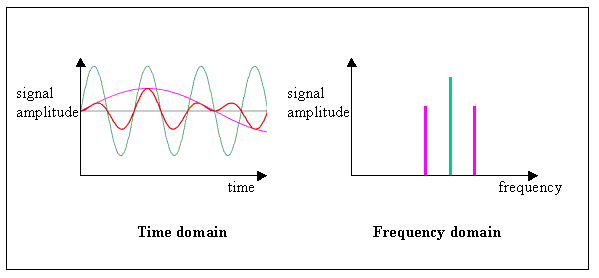
L'intérêt d'utiliser une représentation fréquentielle du signal est de pouvoir identifier les fréquences qui composent le son à un instant précis.
De plus cette représentation permet également de trouver l'intensité des différentes fréquences, ce qui sera très utile pour par la suite analyser les variations importantes dans la musique.

L'implémentation informatique de la transformée de Fourier est un sujet qui a été passé en revue par de nombreux scientifiques et programmeurs auparavant.
Refaire le code d'une telle fonction mériterait probablement un projet à lui seul, et malgré tout, les performances obtenues seraient bien en dessous des implémentations existantes.
La bibliothèque choisie pour calculer la transformée de Fourier du signal audio est "Keep It Simple, Stupid", plus connu sous son acronyme KISS FFT.

Une fois la transformée de Fourier effectuée avec les mille vingt-quatre valeurs décrivant le son à l'instant présent, la fonction retourne une liste de mille vingt-quatre nombre complexes.
Ces nombres complexes sont une représentation du signal dans le domaine des fréquences. Il est alors possible d'en extraire différentes informations telle que l'amplitude des différentes fréquences qui composent le signal.

Pour se faire, il suffit d'appliquer le théorème de Pythagore en utilisant la partie réelle, et la partie complexe, de chacun des éléments de la liste.

Sur la vidéo, il est notable que le fréquence principale du signal audio est représentée par la bande d'indice cinq.
Pour retrouver sa fréquence, il faut diviser le nombre de valeur en sortie de la transformée de Fourier par la fréquence d'échantillonage du fichier audio qui est de 44100Hz, puis multiplier cette valeur par l'indice de la bande.
44 100 / 1024 * 5 ≈ 215Hz
Surprenamment, le résultat est loin des quatre centre quarante Hertz annoncée.
Le problème vient en réalité des données du signal reçues depuis la fonction de rappel. Pour supporter la lecture de fichier stéréo, la bibliothèque STK alterne entre les valeurs destinée au haut-parleur gauche et droit.
Le résultat final possède donc deux valeurs pour chaque fréquence.
C'est pourquoi, pour retrouver la vraie fréquence de chaque bande, il faut diviser la fréquence d'échantillonage par cinq cent douze et non pas par mille vingt-quatre.
Avec cette correction apportée au précédent calcul, il est maintenant clair que le résultat obtenu est correct.

Un autre chose surprenante est le "tremblement" de chaque fréquence malgré l'absence de variation du signal audio.
Ce phénomème s'appelle une "fuite spectrale" et se traduit pas la perte de puissance d'une fréquence donnée vers d'autres cases de fréquence dans la transformée de Fourier.
Le moyen le plus simple pour atténuer ce problème est d'utiliser une fonction de fenêtrage tel que la fonction de Hann. L'usage d'une telle fonction permet de réduire l'influence des fuites spectrales sur le signal final et permet donc d'améliorer la précision du résultat obtenu.

L'application d'une fonction de fenêtrage se fait sur les données reçu par la fonction de rappel (et donc avant le calcul de la transformée de Fourier).

void AudioAnalyzer::applyWindowFunction(std::vector<float>& audioData)
{
  const int sample = 1024;

  // Applying Hanning function
  for (int i = 0; i < audioData.size(); i++)
  {
    audioData[i] = (audioData[i] * (0.5 * (1 - cos(2 * stk::PI * i / (samples - 1)))));
  }
}

La réduction de fuite spectrale est notable et il est clair que le résultat est désormais bien plus stable et précis que précédemment.

Voici maintenant plusieurs exemples utilisant différent morceaux de musique

Il est remarquable qu'une large zone au centre du graphique est inutilisée.
Cela s'explique par le fait que la plupart des fréquences dans une musique ne dépassent pas les neuf KHz. Et comme dit précédemment, la plupart des fréquences sur la seconde moitié du graphique sont des informations redondantes de la première moitié.
Sans les fréquences se situant au-delà de neuf KHz, une légère différence serait audible, cependant pour l'analyse audio, ces informations n'apportent pas d'informations supplémentaires et ne sont donc pas prises en compte.

Maintenant que le signal est filtré et ne contient plus que des informations utiles, il est temps de voir comment analyser un tel signal audio en temps réel.

Détection de variation d'intensité

Ce qui crée le rythme dans une musique c'est sa variation d'intensité.
Si un son continu est joué, auncune variation d'intensité ne sera présente et le son sera alors perçu comme monotone.
C'est donc un changement brut d'intensité par rapport à ce qui vient d'être joué précédemment, qu'il faut détecter.

Il est extrêmement simple d'obtenir l'intensité de la musique à partir des résultat actuels. Pour cela, il suffit de faire la moyenne des amplitudes obtenues.
Afin de savoir si un grand changement d'intensité vient d'avoir lieux, il faut un moyen de comparer cette valeur.
Comme dit précédemment, la notion de "changement brut d'intensité", dépend de ce qui vient d'être entendu par l'oreille.
Il ne faut donc pas comparer l'intensité actuelle avec tout le reste de la musique mais plutôt une petite portion de celle-ci. Cela permet d'être régulier dans l'analyse et éviter qu'un début de musique "mouvementé" ne trouble l'analyze d'une partie plus calme de celle-ci.

Pour conserver les dernières intensités jouées, il faut mettre en place un historique. Sa taille sera de une seconde, ce qui correspond aux quarante trois dernières intensités.
Cela s'explique par le fait que les fichiers audio jouées sont enregistrées à une fréquence de 44100Hz (autrement dit, 44100 valeurs par secondes). Chaque bloc de données étant composé de mille vingt-quatre valeurs, il faut à peu près quantre trois blocs de données (44100 / 1024) pour qu'une seconde s'écoule.

Voici une implémentation basique indiquant qu'une variation d'intensité est présente si la l'intensité actuelle est supérieure à la moyenne de l'historique.

bool findBeat(float currentIntensity, std::vector<float>& intensityHistory)
{
  // Find mean intensity
  float meanIntensity = 0;
  for (int i = 0; i < intensityHistory.size(); i++)
  {
    meanIntensity += intensityHistory[i];
  }
  meanIntensity /= intensityHistory.size();

  // Update intensity history
  intensityHistory.erase(intensityHistory.begin());
  intensityHistory.push_back(currentIntensity);

  // return "true" if a beat is detected
  return currentIntensity > meanIntensity;
}

bool findBeat(float currentIntensity, std::vector<float>& intensityHistory)
{
  ...

  // return "true" if a beat is detected
  const float sensitivity = 1.2f;

  return (currentIntensity / meanIntensity) - sensitivity > 0;
}

Dans les démonstrations suivantes, trois ronds représentent la détection de variation d'intensité avec une différente sensibilité.
Le rond de gauche utilise une sensibilité de 1.2, celui du milieu de 1.4 et le dernier de 1.6.

Avoir cette constante permet certes d'ajuster la sensibilité de la détection de l'algorithme, mais cela manque de régularité.
Dans les exemples précédents, il arrive que la valeur "optimale" diffère selon les passages de la musique.
La musique Wide Instructions possède beaucoup plus de "bruit", rendant la détection de changement d'intensité peu précise avec une basse sensibilité. Le même évênement se produit pendant les vingts premières secondes de la musique M.U.S.H.

Le genre joue beaucoup, une musique du style Rock & Roll contient généralement beaucoup plus de "bruits" et est moins "nette" qu'une musique de style techno, la valeur de la sensibilité devra alors être faible (autour de 1.0), afin de bien détecter les variations de celle-ci.
A l'inverse, pour une musique du genre techno, la valeur de la sensibilité sera plus élevée (autour de 1.4), pour uniquement détecter les variations les plus distinctes.

Pour trouver dynamiquement cette sensibilité, il est possible de se baser sur la variance des intensités stockées dans l'historique.
La variance exprime la moyenne des carrés des écarts à la moyenne, autrement dit, elle indique à quel point les valeurs sont proches de la moyenne.
Plus la variance est élevée, moins le son est "net", et donc plus la valeur de la sensibilité doit être faible pour détecter les variations.

Pour contrôler la sensibilité en fonction de la variance, il est possible d'utiliser une fonction de régression linéaire.
Dans le code suivant, la fonction de régression linéaire rend la sensibilité égale à 1.0 pour une variance de 200, et 1.45 pour une variance de 25.

bool findBeat(float currentIntensity, std::vector<float>& intensityHistory)
{
  ...

  // Find variance
  float variance = 0;
  for (int i = 0; i < intensityHistory.size(); i++)
  {
    float temp = intensityHistory[i] - meanIntensity;
    variance += temp * temp;
  }
  variance /= intensityHistory.size();

  // Find sensitivity
  const float sensitivity = (-0.0025714 * variance) + 1.5142857;

  ...
}

Cette méthode permet donc d'obtenir un indiquateur de changement d'intensité global.
Pour produire les trois ratios mentionnés dans l'introduction, n'avoir qu'un seul indiquateur rend la tâche compliquée, de plus il est évident que cet indicateur manque encore de précision quand le son manque de netteté.
L'idéal serait de pouvoir analyser les variations d'intensité de certaines plages de fréquences en particulier. Ce modèle fournirait bien plus d'informations et permettrait même de déterminer avec précision où se situent les changements d'intensité sur le spectre des fréquences.

Dans la théorie il suffit d'appliquer le même algorithme que précédemment pour chaque amplitude de fréquence.
Au lieu d'utiliser l'intensité moyenne de toutes les amplitudes réunies, chaque amplitude possèdera son propre historique, son intensité moyenne, sa propre variance et sa sensibilité.
Bien qu'un certains nombre d'amplitude ai été supprimé pour cause de données redondantes, cet algorithme devra être appliqué pour quasiment cinq cent amplitudes différentes. Même si les ordinateurs d'aujourd'hui sont de plus en plus puissants, il ne faut pas oublier que la simulation de réaction-diffusion est exécutée de manière simultanée.
De plus, bien qu'un nombre élevé d'indiquateur de changement d'intensité rende l'algorithme plus précis, celui-ci devient alors plus compliqué à adapter et à configurer pour différents genres de musique.
Ici, et pour toute la suite du projet, le nombre d'indiquateur sera de soixante-quatre.

Répartition des différentes fréquences

Jusqu'à présent, l'intensité actuelle de la musique n'était autre que la moyenne de toutes les intensités. Cependant il n'est plus possible d'utiliser cette valeur pour trouver les variations d'intensité de plusieurs plages de fréquences différentes.
Il faut alors trouver un moyen de répartir l'amplitude des différentes fréquences afin d'obtenir soixante-quatre valeurs.

Le moyen le plus simple est de faire une distribution égale de chaque intensité en soixante-quatre valeurs.

Naturellement, le fait d'avoir réduit le nombre d'élément dans le graphique rend le résultat moins détaillé et moins précis.
Mais il y a surtout quelque chose de dérangeant quand à la répartition des intensité. L'utilisation du graphique semble assez inégale, le premier tiers est beacoup plus utilisé que le reste. Ce problème est dû au fonctionnement de l'oreille humaine qui est plus sensible aux basses fréquences. A la place d'une répartition équitable des fréquences, il est préférable d'utiliser une répartition logarithmique. Ce type de répartition permet d'allouer plus d'espace aux basses fréquences sur le graphique en augmentant progressivement le nombre d'intensités par colonne.

L'utilisation de la répartition logarithmique de l'intensité des fréquences rend le résultat bien plus précis, et minimise les pertes d'informations sur les basses fréquences de la musique.
Une dernière modification peut être ajoutée dans le but de faire ressortir l'intensité des hautes fréquences. Au lieu d'utiliser la moyenne de l'intensité des fréquences pour une colonne, il est possible d'uniquement utiliser l'intensité la plus élevée.

Utiliser l'intensité la plus élevée fait ressortir certaines fréquences sur le graphique.
Cette étape n'est pas obligatoire car elle permet certes, de mieux repérer certains changements d'intensités, mais elle augmente également l'influence de divers bruits sur la détection de variations d'intensité.

Maintenant que l'analyse audio possède plusieurs indiquateur de variations d'intensité, et que ceux-ci décrivent les fréquences de la musique de manière optimale, il est temps de les utiliser pour déterminer des informations sur la basse, les cymballes et d'autres sonorités importantes.

Regroupement des variations d'intensité

Quand on regarde l'amplitude des fréquences sur le graphique en même temps que la musique joue, un lien se fait entre ce que l'on entend, et ce que l'on voit sur le graphique.
La basse se situe très souvent, voir toujours dans les toutes premières colonnes.
La grosse caisse, même si son emplacement n'est pas toujours identique, se reconnait à la forme que produisent l'amplitude des fréquences (quelques colonnes formant un dôme). Les cymballes se situent dans la seconde moitié du graphique et forment également un dôme mais avec beaucoup moins d'amplitude.

^{Fréquences habituelles de la basse}

^{Fréquences habituelles de la gross caisse}

^{Fréquences habituelles des cymballes}

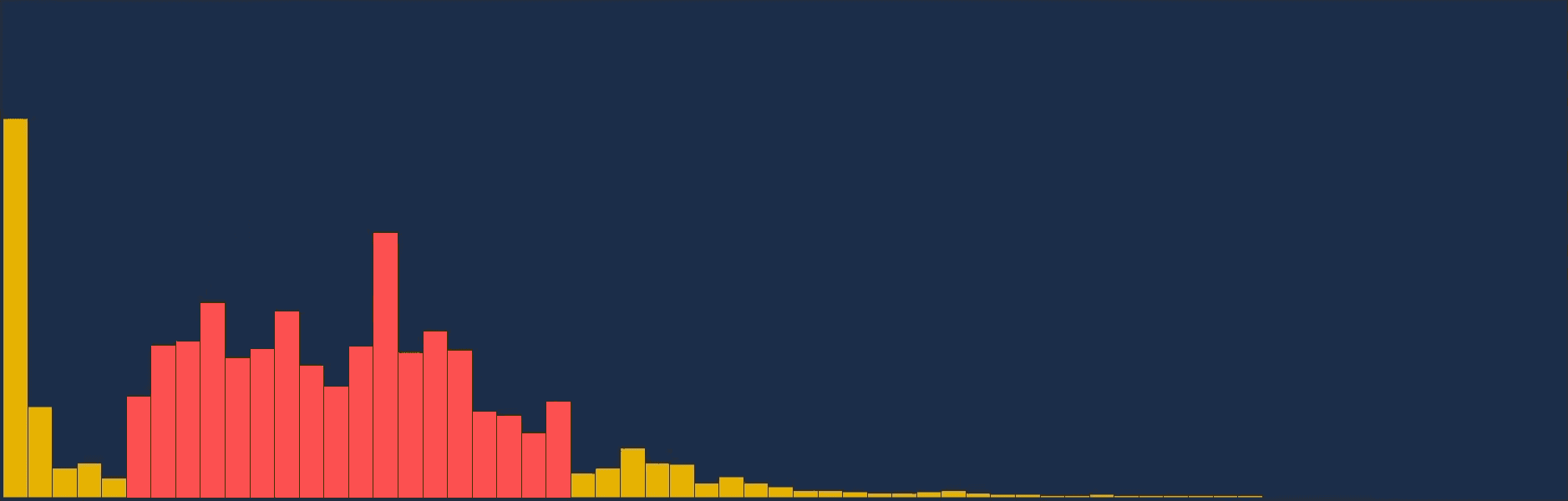
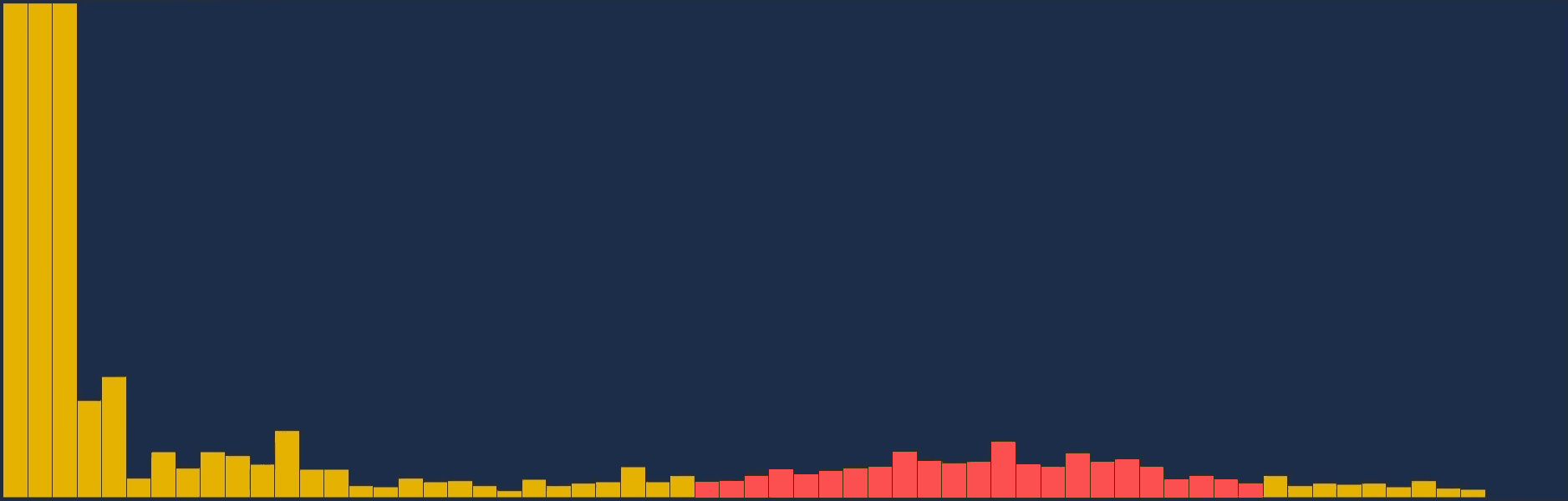
Même si ces sonorités produisent une grande variation d'intensité sur plusieurs colonnes du graphique, il arrive que ces variations proviennent de la même sonorité.
L'objectif ici est de trouver un moyen de regrouper les variations d'intensité détectées, pour ensuite en déduire les ratios correspondants.

Pour identifier et différencier les différents groupes de variations, une classe permet de décrire leurs caractéristiques:

class SoundGroup {
private:
  int _nbElements;
  float _meanIntensity;
  float _meanDelta;
  int _meanIndex;
  int _lastIndexAdded;

public:
  SoundGroup();
  SoundGroup(float newMeanIntensity, float newMeanDelta, int newMeanIndex);

  bool canJoinGroup(float intensity, float delta, int index) const;
  void addToGroup(float intensity, float delta, int index);
};

Une instance de cette classe permet de vérifier si deux variations d'intensité ont une quelconque similitude en comparant leur position dans le domaine des fréquences ainsi que leur intensité.
Si les deux variations d'intensité sont très proche, avec une intensité quasi similaire, il y a de fortes chances pour que ces deux variations proviennent de la même sonorité.
Cette classe fait également l'usage d'un delta, qui n'est autre la différence entre l'intensité actuelle et précédente pour une plage de fréquence. Cette information est très pratique pour savoir si différentes variations d'intensité ont lieu au même moment.

Quand une variation d'intensité est ajoutée, l'instance de la classe met à jour ses membres privées pour qu'ils représentent la moyenne de toutes les variations ajoutées.
Si une variation d'intensité ne correspond à aucun groupe, un nouveau groupe est créé pour elle. Toute les variations d'intensité font donc parti d'un seul et unique groupe.

Posséder cette notion de groupe est avantageux car il est désormais possible d'analyser les variations avec plus d'informations et ainsi d'être sûr qu'il y a bel et bien eu une variation d'intensité.
Si un groupe possède une dizaine de variations d'intensité, et que son delta moyen est très élevé, il y a de forte chance qu'une grande variation d'intensité ait eu lieu.
A l'inverse, il se peut qu'un groupe possède une ou deux variation d'intensité dont la puissance est très faible. Il vaut alors mieux ne pas prendre en compte ce groupe qui a plus de chance d'être du "bruit" qu'une réélle sonorité dans la musique.

Mais surtout ces groupes permettent de désormais identifier les sonorités.
Pour par exemple identifier la basse, il faut un groupe avec une forte intensité et se situant très bas de le domaine des fréquences.

La dernière étape est donc d'enfin déduire le ratio des sonorités ciblées.

Calcul des ratios

L'objectif ici est de vérifier pour chaque groupe si celui correspond aux caractéristiques recherchées.
Tous les groupes déterminés par la partie précédente du programme vont alors être testés afin d'obtenir les différents ratios.

La basse par exemple est toujours située dans les deux premières colonnes du graphique et possède une forte intensité.
Voici un exemple d'implémentation permettant de calculer le ratio de la basse depuis un groupe:

1void findBassRatioFromGroup(SoundGroup& group, float& bassDelta)
2{
3  const float minBassIntensity = 50;
4  const float maxBassIntensity = 150;
5
6  if (group.getMeanIndex() < 2 && group.getMeanIntensity() > minBassIntensity)
7  {
8    if (group.getMeanDelta() > bassDelta)
9    {
10      bassDelta = group.getMeanDelta();
11
12      _bassRatio = group.getMeanIntensity() / (maxBassIntensity - minBassIntensity);
13      if (_bassRatio > 1.0)
14        _bassRatio = 1.0;
15    }
16  }
17}

Les intensités minimales et maximales ont été définies après avoir fait de nombreux tests sur des musiques de tout genre.
La ligne huit permet de conserver le ratio de la basse ayant eu le plus grand changement d'intensité (car il arrive que plusieurs groupes représentent la basse). Si cette valeur est négative, cela veut dire que le son de la basse est en train de diminuer, il est donc important de privilégier le groupe avec le plus grand changement d'intensité.
Le ratio est alors calculé en ramenant l'intensité moyenne du groupe entre zéro et un à l'aide des intensités minimales et maximales.

Le principe est alors le même pour les autres ratios.
Pour les cymballes il faut vérifier que le nombre d'éléments contenu par le groupe est suffisant (généralement entre cinq et quinze). Il faut également veiller à ce que la position moyenne du groupe dans le graphique soit assez élevée (dans la deuxième moitié du graphique).

Le calcul du dernier ratio est un peu plus permissif étant donné qu'il sert principalement à repérer toute variation d'intensité importante n'appartenant pas aux deux premiers ratios.
Celui-ci sera donc plus sensible aux groupes se situant dans la première moitié du graphique et possédant une intensité moins élevée que celle de la basse.

Dans les vidéos suivantes, trois ronds servent à visualiser les ratios calculées. Plus le ratio est proche de un, plus le diamètre du rond associé sera élevé.
De gauche à droite, les ratios sont les suivants : basse, cymballes, sonorité autres.

Malgré la diversité des genres musicaux utilisées, le résultat reste toujours un minimum précis.
Bien sûr, la détection n'est pas parfaite et il arrive qu'un beat soit loupé ou bien qu'un bruit soit considéré comme une variation d'intensité. Cependant, il faut garder en tête que ces ratios seront appliquées aux paramètres de la réaction-diffusion précédemment créée. Et qu'un léger bruit altérant un paramètre pour une fraction de seconde passera inaperçu.
Le fait que la simulation ne soit donc pas aussi sensible que les ronds utilisées en démonstrations permettra d'avoir un résultat plus que satisfaisant dans la prochaine partie.

Conclusion

L'usage d'un algorithme basé sur une approche statistique rend son coût d'exécution relativement faible comparé à un algorithme utilisant des filtres en peignes.
Bien sûr, la précision de ces deux types d'algorithme ne sont pas les mêmes, cependant, pour du temps réel, la précision de l'approche statistique est suffisante.

Les trois ratios mis en place suffisent à détecter les variations d'intensités majeures, pour une grande variété de genres musicaux. Cependant, cet algorithme permet d'aisément ajouter de nouveaux ratios pour identifier des sonorité précises dans une musique.

La dernière étape du projet consiste à trouver un moyen d'assigner ces ratios à diverses propriétés de la réaction-diffusion précédemment créée.

Sources

Frédéric Patin | Beat detection alogrithms : https://www.gamedev.net/articles/programming/math-and-physics/beat-detection-algorithms-r1952/
Wikipédia | Fast Fourier Transform : https://en.wikipedia.org/wiki/Fast_Fourier_transform
Mark Newman | Where is frequency in the output of the FFT? : https://www.youtube.com/watch?v=3aOaUv3s8RY
Ciphrd | Audio analysis for advanced music visualization : https://ciphrd.com/2019/09/01/audio-analysis-for-advanced-music-visualization-pt-1/